Cohomologie cyclique

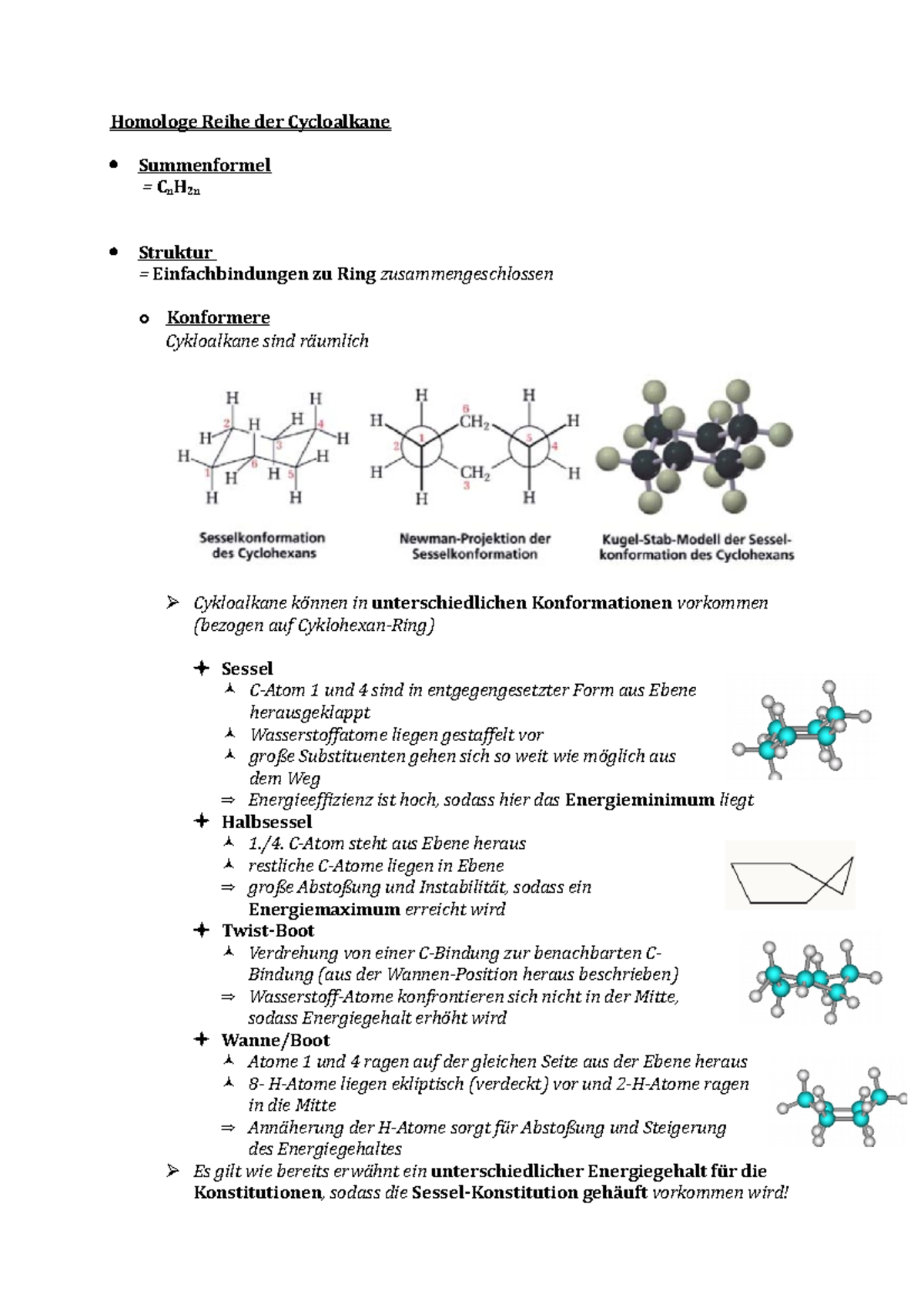
En mathématiques, la cohomologie cyclique d'une ℂ-algèbre ${\displaystyle A}$ (non nécessairement commutative), que l'on note ${\displaystyle HC^{*}(A)}$, est la cohomologie du complexe ${\displaystyle (C_{\lambda }^{n},b)}$ où

• ${\displaystyle C_{\lambda }^{n}}$ est l'espace des formes n 1-linéaires ${\displaystyle \phi }$ qui vérifient la condition de cyclicité :
• l'opérateur ${\displaystyle b:C_{\lambda }^{n}\to C_{\lambda }^{n 1}}$ est l'opérateur de cobord de Hochschild qui est donné par :

Cas des petits degrés

Un 0-cocycle n'est donc rien d'autre qu'une trace. En effet, la condition de cyclicité est automatiquement vérifiée et une forme linéaire sur ${\displaystyle A}$ est un cocycle si et seulement si

En conséquence, la cohomologie de Hochschild et la cohomologie cyclique sont égales en degré 0.

Appariements

Les cocycles cycliques ont la propriété de s'apparier avec les éléments de K-théorie. Plus précisément, il existe une application qui, partant d'un cocycle cyclique et d'un élément de K-théorie de même parité, leur associe un nombre complexe. Cette application est

• bien définie (le nombre complexe ne dépend que des classes en cohomologie cyclique et K-théorie, et non des représentants choisis)
• linéaire en le cocycle
• et additive en l'élément de K-théorie.

Enfin, cet appariement est donné par une formule tout à fait explicite et calculable.

Références

• (en) Alain Connes, Noncommutative Geometry, Academic Press, 1994
• (en) Jean-Louis Loday, Cyclic Homology, Springer, coll. « Grund. der math. Wiss. » (n^o 301), 1998, 2^e éd. (1^re éd. 1992)

• Portail des mathématiques